そもそも公式とは
数学における公式とは正しいと証明された式のうち、覚えて使ったら便利だから数学界で共通認識として証明せずに使って良いものとしようというものです。
つまり便利だから覚えるということが前提です。
しかし、覚えていれば自分で導けなくてOKなのかといえばそれも違います。
丸暗記しただけの公式は、覚えているけどいつ使ったら良いかわからない、使い分けがわからない、少し使っていないと忘れてしまう、といったことが起きてしまいます。
公式は理解をして覚えることが前提なのです。
理解するポイント
漠然と理解するとはいってもイメージがつきにくいと思います。この下の2つの質問に答えられるかどうかを基準に考えてみてください。
- 何を求めるときに使う公式なのか
- どういう流れで導出された式なのか
例:2次方程式の解の公式
実際に2次方程式の解の公式を例に考えてみましょう。
中学の頃は丸暗記をして終わりということも多いと思います。
何を求めるときに使う公式なのか
1つ目「何を求めるときに使う公式なのか」これはもちろん2次方程式ax2+bx+c=0の解を求めたいときに使う公式です。2次関数の交点を求めるといった使い道まで思い浮かべた人もいると思いますが、つまるところax2+bx+c=0の形で表された式のxを求めるために使うという認識でOKです。
どういう流れで導出された式なのか
では2つ目の「どういう流れで導出された式なのか」という点ですが、まずは一度自分の手で導出してみてください。
それでは一緒に見ていきましょう。
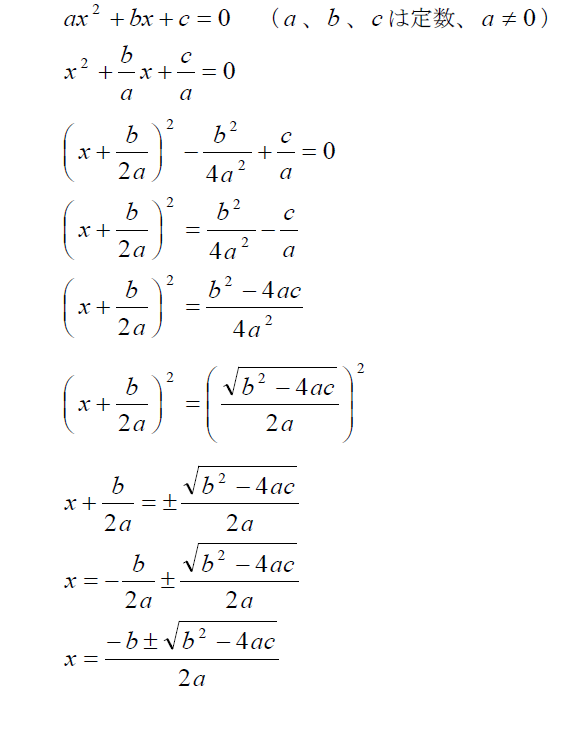
公式は覚えていても意外と苦戦した人も多いと思います。
これがさらっとできた人は理解度MAX!全く問題ありません!
この証明をした人が皆この計算を覚えていたのでしょうか?いいえ、むしろ計算まで含めて覚えていた人は殆どいないでしょう。
今回の例の解の公式の証明で言えば、証明せよと言われれば計算できるが、実際には「元の式を平方完成してったら出る」「途中でどんどん覚えた解の公式の形に揃っていく」という認識くらいだと思います。むしろそこまで理解出来ていれば十分です。
逆にこの流れを理解せずに計算だけ丸暗記しても意味はありません。
結局丸暗記しただけのものは忘れてしまいます。
まとめ
もちろん最初から完璧に公式の意味が理解できている必要はありません。まずは中学生の頃に覚えた解の公式のように「この式で計算すれば2次方程式が解ける」という練習から始めても構いません。しかし、ある程度練習して身についたところで必ず、「じゃあこの式はどこから繋がって出てきたのか」これを確かめるようにしてください。
そうやって「理解して覚えた」公式は忘れることはないし、不安になった時に自分で確かめることが出来ます。
これをするかしないかで公式の理解度、ひいてはその分野の理解度に大きな差が生まれてきます。


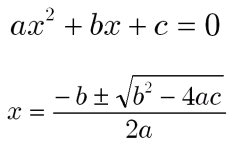


コメント