共通テストの数学の対策を始めると、その長い問題文にまず驚かされると思います。
また、その問題文も理科の問題かと思うような現実の状況が題材として用いられていることにも驚かされるでしょう。
このように、共通テストの数学は難しい、他のテストとはぜんぜん違うと言われていますが、一体どこが難しいのか、何が違うのか見ていきましょう。
共通テスト数学の概要
まずは共通テストの数学の概要です。
- 解答形式:マークシート方式
- 試験科目:数学ⅠA・数学ⅡBCの2科目
- 試験時間:各70分(数学ⅡBCは今年度から70分に)
- 配点:各100点
問題数は数学ⅠAが選択問題なしの全4問必答、数学ⅡBCが6問を選択解答(全7問、第4~7問から3問選択)する形式です。
問題形式だけ見ると、選択問題があるくらいで他のテストと大きく変わりません。
共通テストの難しいポイント
全範囲の出題
大学入試には大学や学部ごとに出題されやすい単元というものがあります。
その点でいうと、共通テストの出題されやすい単元は全単元です。
共通一次試験、センター試験、共通テストと名称や形式を変えて続いてきた試験ですが、教育課程の全部の達成度を測りたいという思いが見えてきます。
全単元から万遍なく出題されるため、苦手単元を作らないということが大切になってきます。
長い問題文と短い解答時間
数学の問題を解くというとき、立式や計算して解き始める前にまず
- 問題文を読み状況を整理する
- ゴールまでの道筋をたてる
- 解き始める
という行程が必要になってきます。
その中の「問題文を読み状況を整理する」という一番のスタートとなるポイントの大前提となる問題文が、他の大学入試やセンター試験と比べて非常に長く、難しくなっています。
これはセンター試験とよく比較されますが、センター試験時代20ページほどであった数学ⅠAが、2023年度では26ページ、最新の2024年度では29ページと試験時間の10分増を考慮したとしても、その文章量は非常に多くなっています。
また、これほどのページ数となる数学の問題は他の国公私大のどこにも見られるものではありません。
また、比較したセンター試験から試験時間は10分増加し70分になりましたが、それを考慮しても、問題文が長く、難しくなっているため、非常に時間制限が厳しくなっています。
いろいろな出題パターン
このように問題が長くなって制限時間が厳しい共通テストですが、問題を読み解くことを難しくしているもののもう1つとして、出題形式が多様化している点が挙げられます。
現実のテーマに即した出題
数学の問題としてよく出題されるように、数字や文字・記号で完全に抽象化された状況ではなく、日常的なテーマを題材として、それらに関する数学的な考察を行わせる出題があります。
直接的な理科の知識が必要となるわけではありませんが、三角比を用いて長さを表現したり、物体の運動を関数でとらえたりといった経験の多い物理選択者がイメージしやすいものも多く出題されています。
(近年の出題例)
- 短距離走のタイムとストライド・ピッチとの関係(2次関数)(2021)
- 地図アプリから山頂を見上げる角度を求める(三角比)(2022)
- シュートされたバスケットボールの軌道(2次関数)(2023)
- 太陽高度と電柱の影の長さ(三角比)(2024)
グラフに関する問題
共通テストの数学ではグラフの形の変化を答えさせる問題も出題されています。
記述式の問題でグラフを書かせる問題は出題されていますが、グラフの動きや変化を選ばせると言う問題はほかで見られない共通テスト特有の問題と言えるでしょう。

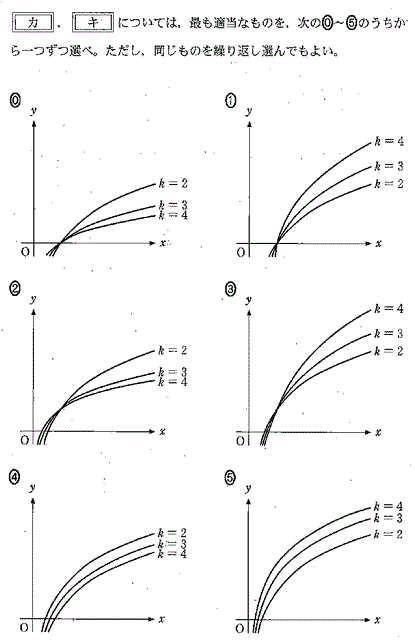
このように扱われる状況や、問われているものが他の試験では見られない、問題をパターン化して解くことが難しいものになっています。
共通テスト数学の対策
このように難しいと言われている共通テスト数学ですが、このために何か特別な対策が必要なのか?
答えはNOです。
もちろんこの特殊な形式に慣れる練習は必要ですが、まず土台となる数学力を鍛える必要があります。
時間が足りない、知っている解き方の問題なのに解き方に気付けない。
こういうときに共通して起きていることとして基礎の理解・定着の甘さがあります。
皆さんの多くが、チャート式、フォーカスゴールドなどの基本問題集を使って勉強していると思いますが、その各ページの問題文を見たときに
- 何を求めるor何をする問題なのか
- どのような順で解いていくのか
このような問題の発想点を問題文を読んだ瞬間に説明できるようになっているかをやってみてください。
点数が伸び悩んでいる単元は、「えっと、、、、、最初ここから計算するけどなんでだっけ?」と言うように問題の理解、解法の定着が甘い問題が多くあるはずです。
そういった問題は改めて解いて解答解説を読み返し復習しましょう。
それを繰り返してすべての問題で説明できるようになった時、あなたの数学力は大きく伸びています。
そうなれば、新しい問題に触れたときも、発想点がどこなのか考える力が身についているため解けば解くほど考え方が整理されていきます。





コメント