数学をやっていて嬉しい瞬間は?
数学が好きな人に「数学をやっていて嬉しい瞬間は?」と聞くと「問題が解けた時」という答えが多く上がると思います。
ですが、数学が嫌いな人も今までに数多く問題を解いてきた経験があるはずです。
そこにはどんな差があるのでしょうか。
問題が解けて「楽しい」という人の意識には往々にして「理解して解けている」というものが含まれています。
では「理解して解ける」というのは一体どういうことでしょうか。
- 何を求める(示す)問題かわかる
- 使っている公式の意味がわかる
- 手順の意図がわかる
この3つを見て当たり前だと思うかもしれません。
どれだけ難しい問題を解けていても、何を求めているかもわからず、ただ手順や公式を丸暗記して当てはめているだけでは楽しいなんて思えるはずもありません。むしろただただ面倒な作業をさせられているだけに思えてしまっても当然でしょう。
それでは実際に問題を見てみましょう。
例題:【2次関数の最大・最小の問題】

手順の確認
まずは手順を見てみましょう。
- 平方完成する
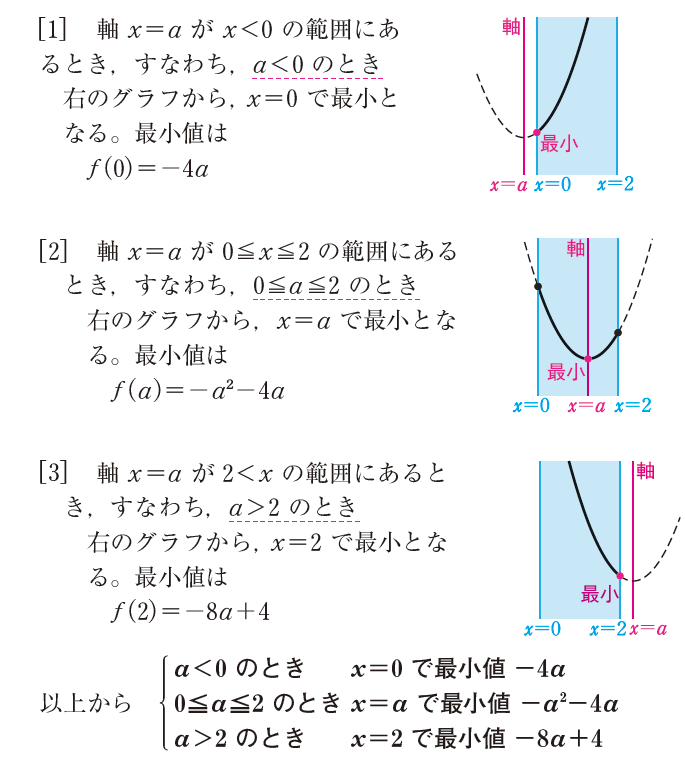
- a<0、0≦a≦2、a>2で場合分けをする
- それぞれの場合のグラフを描く
- それぞれの場合での最小値を求める
この4つが大きな流れになりますが、これらの手順にはどんな意図が含まれているか確認してみましょう。
手順を理解する
- 平方完成するのはなぜ?
→頂点の位置によって最小値が変わるからまず頂点を求める。 - 場合分けをするのはなぜ?
→頂点が定義域の右、内部、左のどこにいるかで最小値が変わるから。 - なぜグラフが必要?
→それぞれの場合の値の大小関係を見た目でわかりやすく判断するためにグラフを描く。 - ここまで来たら各場合の最小値を書き上げるだけ!
ここまで詳細に言語化していなくても、ただ手順を覚えているだけじゃなく理解して解いている人は概ね同じようなイメージを持っているはずです。
そういう人であればパターンの違う類題にあたっても解ける、もしくは解答解説から例題と類題との違いを理解して覚えられます。
高校数学は中学数学と違って一つのパターンにつき同じような類題を何度も何度も繰り返すことは多くありません。
そのためこの「理解して解く」ことが出来ているかどうかが大きな差になります。
問題が解けた時、そこに「理解」出来ていたかをちょっと立ち止まって意識してみてください。
一つ一つの問題を理解して数学を楽しいと思えた時、あなたの数学力は確実に成長していきます。




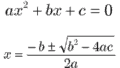
コメント